The elements of statistical learning 리뷰 2단원(1)
벌써부터 어려워진다.. 영어라서.. 한글이면 어떻게든 할텐데...ㅜㅜ
2. overview of supervised learning
2.1 도입
챕터 1에서 train 데이터라고 불리는 것은 특성들과 outcome들이 붙어있고
이 train 데이터를 input으로 넣어서 output을 예측하는 것이 목적이라고 했어.
그리고 이걸 supervised learning이라고 불렀지.
2.2 변수타입과 용어
inputrhk output의 타입이 무엇이냐에 따라 분석방법과 예측방법이 달라지므로 타입을 분류하는 것이 중요하다.
예를 들어 연속적인 출력을 예측할 때는 보통 회귀라는 방식을 사용하고 이산적인 출력을 예측할 때는 분류라는 방식을 사용한다.
- 연속적인 변수(quantitative variables) : 연속적인 데이터들을 말한다.
- 이산적인 변수(qualitative variables) : 예를 들어 멤버의 수, 성공/실패, 1/0, dummy variables, discrete variables, categorical 이라고도 부른다.
- 순서형 변수(ordered categorical) : 이산적인 변수에 순서가 있는 것을 말한다. 예를 들어 small, medium, large.
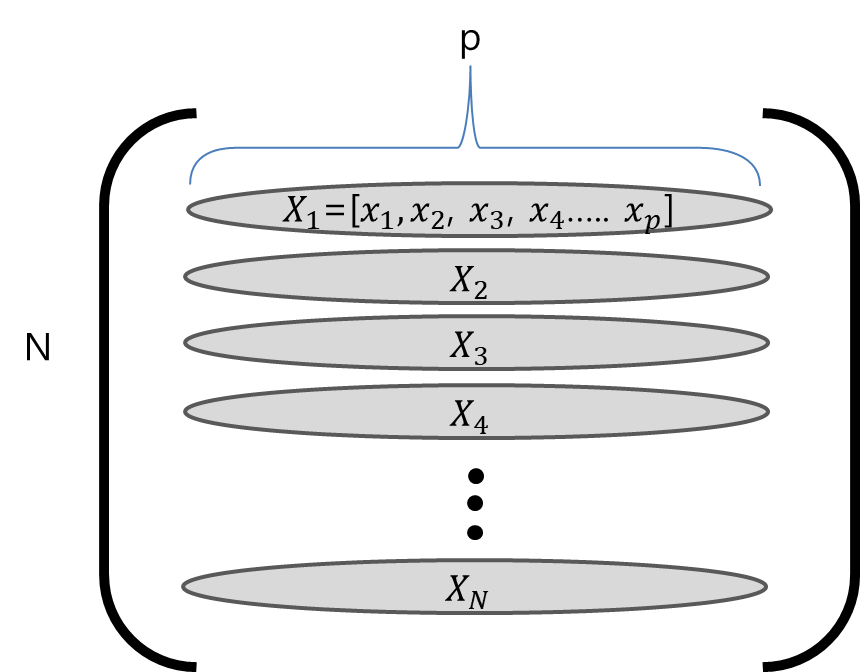
이제부터 input 변수들을 X라고 부르고 X가 벡터이면 Xj라고 부른다.
연속적인 output이면 Y이고 이산적인 output이면 G라고 한다.
실제 관찰되거나 측정된 값든은 소문자 x로 표시되고 i번째 값을 xi라고 부른다.
이 xi는 스칼라, 벡터 모두 가능하다.
2.3 예측에 대한 두가지 접근(least squares, nearest neighbors)
이제 least squares와 k-nearest-neighbor 으로 학습되는 선형모델을 만들것이다.
선형모델은 큰 가정을 하고있기에 수식적으로나 구조적으로 안정적이지만 이 모델을 통한 예측은 부정확하다.
k-nearest-neighbor의 방법은 가벼운 가정을 가지고 있어 수식적으로 불안전하지만 그것의 예측은 종종 잘 맞아떨어진다.
선형모델과 least squares
선형모델에 들어가는 input X를 이용하여 우리는 output Y를 추정할 것이다. 이 추정한 Y를 Y hat이라고 표현한다.
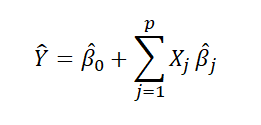
이런 식으로 표현 가능하고 더 간단히 나타내기위해 베타 제로를 시그마 안에 넣는다.
그러기 위해서는 X에 상수인 1을 추가하면 된다.

이 식으로 우리는 선형모델을 만들었다.
이제 선형모델에 train 데이터를 어떻게 적합시킬수 있을까?
즉 우리가 만든 선형모델에 이 train 데이터를 이용하여 어떻게 맞출수있을까?
그리하여 이 선형모델이 어떤 현상을 예측할 수 있을까?
가장 유명한 방식이 least squares 방식이다. 간단히 말해서 오차를 최소화하는 방식이다.
실제 결과와 우리가 예측한 결과의 차이를 제곱해서 이 오차가 최소인 지점을 찾는 방식을 말한다.
식으로 표현하면
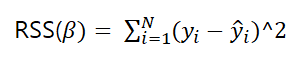

행렬미분을 한다.

이 성질을 이용하면

이런 결과가 나온다. 여기서 나온 베타에 의해 우리가 추정하는 y hat이 달라지고
이 말은 베타를 잘 설정하면 오차를 줄일 수 있다는 말이 된다.
nearest-neighbor 방법
이 방법은 관측치들 즉 y를 이용하는 방법이다.
input이 들어왔을 때 train 데이터를 기준으로 가까운 데이터로 그 데이터를 판단하겠다는 것이다.
k-nearest-neighbor, 즉 그 지점에서 가까운 k개의 데이터를 살펴보고 많이 나온 것으로 판단하는 방법이다.
예를 들어 k= 5일 때 그 지점에서 가까운 5개의 데이터가 [오렌지색, 파란색, 오렌지색, 오렌지색, 파란색]이라고 하면
그 점을 오렌지색이라고 판단하는 것이다. 여기서 말하는 가까운이라는 것은 유클리드 거리공식을 이용해도 되고 코사인유사를 이용해도 되고 선형모델을 사용하는 사람의 판단에 맡긴다.
least squares vs nearest neighbors
least square를 이용한 선형 결정경계는 매끄럽고 적합시키는 것이 안정적이다.
least square의 선형 결정경계는 수식에 심하게 의존하고 있고 낮은 분산과 높은 편향을 가지고 있다.
반면에 k-nearest-neighbor은 수식에 그렇게 강하게 의존하지 않지만 어떤 특정한 부분에서 적은 수의 데이터로 판단하기도 하고 이로 인해 꾸불꾸불 거리고 불안정하다. 다시 말해 높은 분산과 낮은 편향을 가지고 있다고 할 수 있다.
통계적 결정 이론
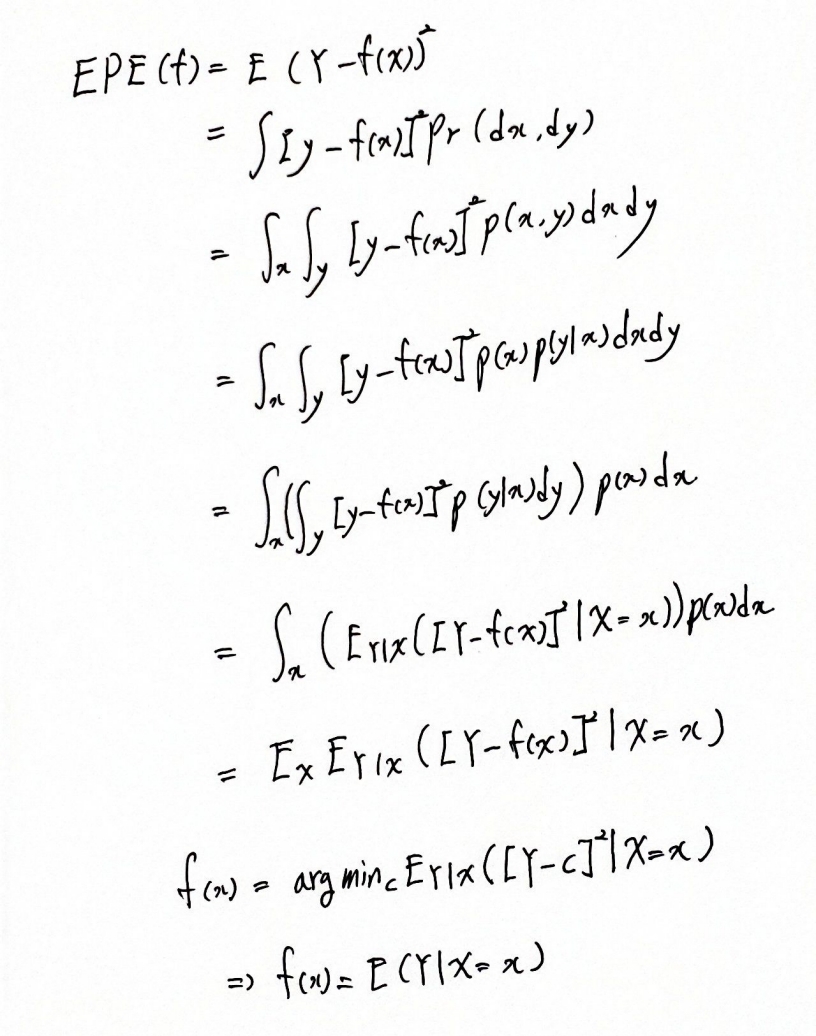
EPE가 이렇게 변한되는 것은 확률밀도함수의 정의로 변환되고
EPE를 최소화해야 우리가 추정하는 f(x)들이 정답을 잘 맞춘다는 의미가 돼!!!
즉 EPE를 최소화하는 f 를 찾아야한다는 것!! 이런 의미로 argmin이 나온것이다.
솔루션은 X=x 일때 Y가 되면 이 값이 최소가 되는 거지.
즉 간단히 애러가 최소가 되는 값은 그 값을 맞추는 거지. 즉 애러가 0이 된다는 것이고
이 말처럼 f(x)가 저렇게 결정된다는 의미!!!!
이 함수는 회귀함수라고도 알려져있는거지~
nearest-neighbor 방법도 이 수식을 이용해서 결정된다.
다만 f(x)의 표현과 두 가지 가정이 추가된다.

Ave는 평균을 의미하고 Nk 는 k 지점에서 인접한 데이터들의 집합을 의미한다.
두 가지 가정이란
첫번째 기대값들은 샘플데이터들을 평균으로 근사화된다.
두번째 한 포인트에 맞춰진다는 의미는 그 포인트에 가까워진다는 의미이다.
이 두가지 가정과 위의 수식으로 nearest-neighbor 도 결정된다.
데이터가 커지면 커질수록 모델은 안정적이고 적합하다.
즉 N,k -> 무한대 일수록 f hat이 E(Y|X=x)로 추정된다. 우리의 결정이론과 부합하는 결과로 향한다.
하지만!!! 실제로 데이터는 한정적이다. 무한대의 데이터를 얻을 수 없으므로 결정이론을 그대로 적용할 수 없고 여러 문제가 발생한다.
이러한 문제들은 나중에 조금 더 살펴볼 것이고 이 문제들 때문에 차원이 증가함에 따라 수렴의 밀집도가 떨어진다.
이러한 환경에서 회귀는 어떤 방식으로 적합시킬 것인가??
회귀에서는

f(x)를 위의 식으로 가정하여 모델링을 하고 이 식을 EPE에 넣고 구함으로써
베타를 구할 수 있다.
결과적으로
KNN 과 Least squares 모두 평균에 의해서 조건적 기대값들을 근사화하는 것으로 끝난다.
하지만 이 두 가지 모델은 가정에서 큰 차이점이 있다.
Least squares 는 전체적으로 회귀함수에 의해서 잘 근사화되어있고
KNN은 부분적으로 상수 함수에 의해 근사화되었다는 점이다.
KNN이 더 맘에 들것이지만 최근의 기법들은 대부분 Least squares를 쓰고 있다.
추가적으로
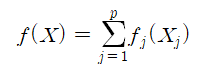
f(X)를 회귀모델들의 합으로 나타낼 것이다.
현재까지 loss function을 L2를 사용하고 있는데 L1을 사용해도 되긴 해
하지만 현재 많이 사용되고 있는 것은 L2이다. L1이 불연속이여서 L2를 사용한다고 생각하자.
또한 만약 output이 범주형이면 결정이론을 어떤 방식으로 할 것이냐?
이는 똑같이 적용하면 된다. 다만 수식만 변경된다.

이 해법을 Bayes classifier 라고 하며 Bayes classifier의 error rate를 Bayes rate라고 한다.
여기까지 1차로 마무리할게.
이해하는 데도 시간이 걸리고 너무 어려운 책이야..